Vedic Mathematics is the name given to the ancient system of Mathematics which was rediscovered from the Vedas between 1911 and 1918 by Sri Bharati Krsna Tirthaji (1884-1960). At the beginning of the twentieth century, when there was a great interest in the Sanskrit texts in Europe, Bharati Krsna Swamiji tells us some scholars ridiculed certain texts which were headed 'Ganita Sutras'- which means mathematics.

1. High Speed Vedic Mathematics is 10-15 times faster than normal Maths

2. Better and Much Improved Academic Performance in school and Instant Results

3. Sharpens your mind, increases mental agility and intelligence

4. A Complete System comprising all the benefits of Mental Maths .

 Learn how to multiply numbers through easier mathods for an examples 

65X65=4225 , 95X95=9025, 105X105=11025(6x7=42 and write square of 5 i.e., 25 then it becomes 4225 similarly for those numbers who ends with 5)

 111X111=12321 (within seconds) many more multiplications like 679x567=  ............  by following method .I have used sargam for indicating multiplication like sa(vertical),re(cross), ga(cross then vertical) as given below:

For two digit numbers , sa (vertical multiplication) , re (cross) then apply sa.

There are 3 steps:

a) Multiply vertically on the left: 2 x 2 = 4.

    This gives the first figure of the answer.
b) Multiply crosswise and add: 2 x 3 + 1 x 2 = 8
    This gives the middle figure.
c) Multiply vertically on the right: 1 x 3 = 3
    This gives the last figure of the answer.

             For three digit numbers , we shall applt sa(1) , re(2), ga(3) ,re(4) then sa(5)  ----as shown above

     

                  

Let us work another problem by placing the carried over digits under the first row and proceed.


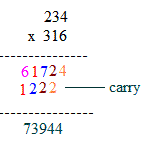
Steps:

i) 4 X 6 = 24 : 2, the carried over digit is placed below the second digit.
ii) (3 X 6) + (4 x 1) = 18 + 4 = 22 ; 2, the carried over digit is placed below third digit.
iii) (2 X 6) + (3 X 1) + (4 X 3) = 12 + 3 + 12 = 27 ; 2, the carried over digit is placed below fourth digit.
iv) (2 X 1) + ( 3 X 3) = 2 + 9 = 11; 1, the carried over digit is placed below fifth digit.
v) ( 2 X 3 ) = 6.
vi) Respective digits are added.

Another way to multiply just over 100

• 103 x 104 = 10712 The answer is in two parts: 107 and 12,
  107 is just 103 + 4 (or 104 + 3),
  and 12 is just 3 x 4.
• Similarly 107 x 106 = 11342 107 + 6 = 113 and 7 x 6 = 42
• Method for multiplying numbers where the first figures are the same and the last figures add up to 10.
  
  • 32 x 38 = 1216 Both numbers here start with 3 and the last
    figures (2 and 8) add up to 10.
    So we just multiply 3 by 4 (the next number up)
    to get 12 for the first part of the answer.
    And we multiply the last figures: 2 x 8 = 16 to
    get the last part of the answer.
    Diagrammatically:
    
  • And 81 x 89 = 7209
  
  
  • Multiplying a number by 11.
  • To multiply any 2-figure number by 11 we just put the total of the two figures between the 2 figures.
    • 26 x 11 = 286 Notice that the outer figures in 286 are the 26
      being multiplied.
      And the middle figure is just 2 and 6 added up.
    • So 72 x 11 = 792